Урок N 19

Данные логического, символьного и строкового типа в Turbo Pascal.

Библиотека (модуль) CRT и Graph.

Работа с файлами в Turbo Pascal.

Построение графиков функций. Численные методы.

Логический тип переменных называется булевым. Он основан на ма-

тематической логике, в которой применяются две константы: 1 (ис-

тина) и 0 (ложь). В языке Turbo Pascal тоже есть две логические

константы: TRUE (истина) и FALSE (ложь). Их можно использовать в

явном виде или обозначать именем в разделе CONST, например:

const

T=true;

F=false;

L=true;

Логическая переменная тоже может принимать два значения TRUE и

FALSE. Описание логической переменной имеет тип BOOLEAN, например:

var L,A,C:boolean;

В разделе операторов логическому типу переменной можно присвоить

значение логической константы, например:

L1:=true; L2:=false; L3:=L1;

В языке Turbo Pascal для сравнения переменных, принимающих чис-

ленные значения, существуют следующие операции отношений:

 

< меньше,

<= меньше или равно,

= равно,

<> не равно,

> больше,

>= больше или равно.

 

Операции с данными логического типа

 

В языке Turbo Pascal есть логические операции:

OR - логическое ИЛИ (логическое сложение - дизъюнкция).

AND - логическое И (логическое умножение - конъюнкция).

NOT - логическое отрицание НЕ.

 

Пример программы с использованием логических операций.

Задача. Дополните программу вычисления площади треугольника по

формуле Герона исследованием существования треугольника, если

заданы его три стороны.

 

program tangle;

var a,b,c,p,S,Q:real;

begin

writeln('Вычислите площадь треугольника по трем сторонам');

writeln('и проведите его анализ.');

writeln('Введите стороны треугольника a,b,c:');

read(a,b,c);

p:=(a+b+c)/2;

S:=sqrt(abs(p*(p-a)*(p-b)*(p-c)));

if (a>=(b+c)) or (b>=(a+c)) or (c>=(a+b))

then writeln('Треугольник не существует.')

else if (a=b) and (b=c)

then writeln('Треугольник равносторонний, его площадь S=',s)

else if (a=b) or (b=c) or (a=c)

then writeln('Треугольник равнобедренный, его площадь S=',s)

else writeln('Треугольник разносторонний, его площадь S=',s);

if (a*a=(b*b+c*c)) or (b*b=(a*a+c*c)) or (c*c=(a*a+b*b))

then writeln('Треугольник прямоугольный.');

writeln('Для выхода из программы введите число 1.');

readln(Q);

end.

 

Данные символьного типа в Turbo Pascal Язык TP может обрабатывать не только числа, но и символы. Это даёт возможность представлять в программах тексты и выполнять над ними некоторые операции, обрабатывать различные ведомости, доку- менты, справочники и т.д. Значениями символьного типа является всё множество символов ПК. Каждому символу приписывается целое число в диапазоне 0...255. Это число служит кодом внутреннего представления символов. Для кодировки используется код ASCII (Американский стандартный код для обмена информацией). Символьная константа (литера) - это символ, заключенный в апост- рофы, например: 'A', 'R', '+', '7'. Внешние апострофы являются признаком символьной константы, которая занимает 1 байт памяти. Символьную константу можно обозначить именем и задать в разделе констант, например: Const sim='A'; A='B'; S='+'; D1='T'; Символьная переменная принимает значение одного символа. В раз- деле переменных она обозначается описателем CHAR (символьный тип), например: Var B1,B2,R:CHAR; BUKVA:CHAR; Допускается использование символьных данных в операторе присваи- вания, например: BUKVA:='A'; R:='*'; B1:='S'; Операции. Так как символы языка упорядочены, то к символьным данным применимы операции отношений (сравнений): <,<=,=,<>,>,>=. Поэтому 'A'<'B'; '+'<'-'; '*'<'4'. Результатом операции сравнения является логическая константа TRUE (истина) или FALSE (ложь). К символьным данным можно применять встроенные функции: ORD(X)-определяет порядковый номер символа X, например ORD('R')=82. CHR(X)-определяет символ, стоящий по порядковому номеру Х, напри- мер: CHR(68)='D'; PRED(X)-определяет предыдущий символ по отношению к Х, например: PRED('N')='M'; SUCC(X)-определяет последующий символ по отношению к Х, например: SUCC('R')='S'.   Пример программы вывода на экран символов (букв) от A до Z:   program Simbol; {Данные символьного типа} uses crt; var i:Char; begin clrscr; writeln('Вывод на экран букв от A до Z:'); for i:='A' to 'Z' do write(' ',i); writeln; writeln('Выход-любая клавиша.'); readkey; end.

Строковые данные Строковые данные - это последовательность символов произвольной длины (до 255 символов). Размер строки указывают в квадратных скобках, но если размер не указан, то он считается равным 255. Строковые данные задаются описателем string. Пример строковой пе- ременной: var str1: string[80]; str2: string;   Строковая константа: const January: string[10]='Январь';   Для строковых данных применимы операции объединения (конкатена- ции) и сравнения. Пример: Объединение двух строк. program ObStr; var str, str1, str2: string[80]; begin .... str1:='Turbo'; str2:='Pascal'; str:=str1+str2; {В переменной str - 'Turbo Pascal'} .... end.   Пример программы, позволяющей соединить два слова в одно:   program Stroka1; {Строковые переменные} uses crt; var x,y,z:string[255]; begin clrscr; writeln('Программа, объединяющая два слова в одно.'); writeln('Введите 1-е слово:'); readln(x); writeln('Введите 2-е слово:'); readln(y); z:=x+y; writeln(z); writeln('Выход-любая клавиша.'); readkey; end.

Библиотека (модуль) CRT в Turbo Pascal.   Библиотека CRT позволяет менять цвета и яркость экрана, производить его очистку, управлять звуковым генератором компьютера. Подключение модуля CRT производится директивой USES CRT, которая указывается в разделе описаний. CRT - аббревиатура, означающая "Электронно-лучевая трубка".   Таблица настройки цветов в модуле CRT Turbo Pascal Константа Число Цвет Процедуры Black 0 Черный TextColor, TextBackGround Blue 1 Синий TextColor, TextBackGround Green 2 Зеленый TextColor, TextBackGround Cyan 3 Голубой TextColor, TextBackGround Red 4 Красный TextColor, TextBackGround Magenta 5 Фиолетовый TextColor, TextBackGround Brown 6 Коричневый TextColor, TextBackGround LightGray 7 Ярко-серый TextColor, TextBackGround DarkGray 8 Темно-серый TextColor LightBlue 9 Ярко-синий TextColor LightGreen 10 Ярко-зеленый TextColor LightCyan 11 Ярко-голубой TextColor LightRed 12 Ярко-красный TextColor LightMagenta 13 Ярко-фиолетовый TextColor Yellow 14 Желтый TextColor White 15 Белый TextColor Blink 128 Мерцание TextColor (как слогаемое)

Основные директивы модуля CRT Uses CRT - подключение модуля CRT. TextColor - устанавливает цвет символов. TextBackGround - устанавливает цвет фона (только 8 неярких цветов). HighVideo - устанавливает включение яркости. LowVideo - устанавливает выбор низкой яркости. NormVideo - восстановление того цветового оформления, которое было на момент начала работы программы. ClrScr - производит очистку экрана. ReadKey - обеспечивает задержку изображения и выход из программы при нажатии любой клавиши, например Esc, Enter, Пробел. Sound(1000) - включение звукового сигнала частотой 1000 Гц. Sound(1500) - включение звукового сигнала частотой 1500 Гц. Delay(1000) - установка (задержка) звучания на время 1 с (1000 мс). Delay(2000) - установка (задержка) звучания на время 2 с. NoSound - отключение звукового сигнала. Пример подключения модуля CRT: USES CRT; BEGIN TextColor(14); {Задаёт желтые символы текста} TextBackGround(5); {Задаёт фиолетовый фон} HighVideo; {Устанавливает включение яркости} ClrScr; {Очищает экран}   Пример: TextColor(14+128); {Задаёт мерцание символов желтого цвета}   Пример программы, использующей модуль CRT:   Program Gas; uses CRT; var N:integer; begin TextColor(14); TextBackGround(1); highvideo; clrscr; writeln('Законы состояния идеального газа.'); writeln; writeln('Рассмотрим случаи (здесь число N - номер случая), когда:'); writeln('1) T=const, N=1.'); writeln('2) V=const, N=2.'); writeln('3) P=const, N=3.'); writeln('4) P,V,T=varia, N=4.'); writeln('5) Быстрое сжатие или расширение'); writeln('в теплоизолированном сосуде Q=0, N=5.'); write('Введите число N='); read(N); writeln; if N=1 then writeln('Изотерм. процесс, T=const, PV=const-закон Бойля-Мариотта.'); if N=2 then writeln('Изохорный процесс, V=const, P/T=const-закон Шарля.'); if N=3 then writeln('Изобарный процесс, P=const, V/T=const-закон Гей-Люсака.'); if N=4 then writeln('P,V,T=varia, PV=(M/Mo)RT-уравнение Менделеева-Клайперона.'); if N=5 then writeln('Адиабатный процесс, Q=0, (PV)Г-уравнение Пуассона.'); if N>5 then writeln('Другие случаи здесь не рассматриваются.') else writeln; writeln('Выход - любая клавиша.'); readkey; TextColor(7); TextBackGround(0); clrscr; end.

Библиотека (модуль) Graph в Turbo Pascal 7.0. Модуль Graph представляет собой библиотеку подпрограмм Turbo Pascal, обеспечивающих полное управление графическими режимами различных мониторов - CGA, EGA, VGA, SVGA. Библиотека содержит более 50 графических процедур и функций, как базовых (рисование точек, линий, окружностей и т.п.), так и расширяющих возможностей базовых (многоугольники, закрашивание фигур, вывод текста и др.). Для запуска программ, использующих модуль Graph, должен быть доступен драйвер egavga.bgi. Для компиляции программ должен быть доступен модуль GRAPH.TPU.   Основные директивы модуля GRAPH Uses GRAPH - подключение модуля GRAPH. InitGraph(gd,gm,'c:\tp7\') - инициирование графического режима, указываем gd-графический драйвер, gm-графическую мода и полный путь файла поддержки графики egavga.bgi: c:\tp7\. ClearDevice - очистка экрана в графическом режиме. SetColor(14) - установка цвета рисуемых линий. SetBkColor(1) - установка цвета фона. SetLineStyle(0,0,3) - установка толщины линий. SetFillStyle(5,11) - установка стиля и цвета закраски. Число сти- лей закраски = 0-11. PutPixel(300,250,15) - рисование точки (X, Y, C), где X, Y -коор- динаты точки, C - цвет точки. С=0-15. Line(25,100,100,200) - рисование отрезка прямой линии (X1,Y1,X2,Y2), где X1,Y1-координаты начала отрезка; X2,Y2-коор- динаты конца отрезка прямой линии. Rectangle(25,100,100,200) - рисование прямоугольной рамки (X1,Y1,X2,Y2), где X1,Y1 и X2,Y2 - координаты соответственно начала и конца диагонали левого верхнего угла. Bar(20,70,210,50) - рисование закрашеннго прямоугольника (X1,Y1,X2,Y2), где X1,Y1 и X2,Y2 - координаты соответственно начала и конца диагонали левого верхнего угла. Circle(300,250,80) - рисование окружности (X, Y, R), где X, Y - координаты центра окружности, R - радиус окружности. Arc(300,250,135,45,60) - рисование дуги окружности (X,Y,Ф1,Ф2,R), где Ф1,Ф2 - начальный и конечный углы дуги. X,Y,R - см. выше. PieSlice(100,100,30,120,70) - рисование сектора окружности (X,Y,Ф1,Ф2,R). Ellipse(300,250,0,360,95,40)-рисование эллипса (X,Y,Ф1,Ф2,R1,R2). Ф1,Ф2 - начальный и конечный углы. R1, R2 - радиусы эллипса. Sector(400,100,90,290,200,80)- рисование сектора эллипса (X,Y,Ф1,Ф2,R1,R2). FillEllipse(X,Y,R1,R2) - рисование закрашенного эллипса (или окружности при R1=R2). OutTextXY(25,30,'Текст.') - вывод текста (X, Y, 'Текст'). CloseGraph - закрытие графического режима.   Ниже приведены примеры программ, использующих модуль Graph и Graph0 (модуль Graph0 - графика для начинающих, упрощенный модуль Graph). Из комментариев к ним можно узнать о конкретном использо- вании основных директив модуля Graph при создании простейших гра- фических изображений.   Пример 1.   Program Ris1; uses Crt,Graph; var gd,gm:integer; {gd-графический драйвер, gm-графическая мода} begin gd:=detect; {Автоматически определяем графический драйвер} InitGraph(gd,gm,'c:\tp7\'); {Инициируем графический режим, указы- ваем полный путь файла egavga.bgi} SetLineStyle(0,0,3); {Задаем толщину линии} SetColor(LightMagenta); {Задаем цвет линии} SetFillStyle(1,LightGreen); {Задаем стиль и цвет закраски} PieSlice(100,100,30,120,70); {Рисуем сектор окружности, X,Y,Ф1,Ф2,R} SetColor(White); {Задаем цвет линии} SetFillStyle(5,11); {Задаем стиль и цвет закраски} Sector(400,100,90,290,200,80); {Рисуем сектор эллипса, X,Y,Ф1,Ф2,R1,R2} Readkey; {Обеспечиваем задержку изображения и выход из программы при нажатии любой клавиши, например Esc, Enter, Пробела} CloseGraph {Закрываем графический режим} end.   Пример 2.   Program Grafika; uses Crt,Graph,Graph0; {Подключаем модули CRT, GRAPH, GRAPH0} begin Init('c:\tp7\'); {Указываем полный путь файла egavga.bgi} SetColor(14); {Задаем цвет рисуемых линий} SetLineStyle(1,0,ThickWidth); {Задаем тройную толщину линии} SetBkColor(1); {Задаем цвет фона} Circle(300,250,120); {Рисуем окружность, X, Y, R} SetColor(11); Circle(300,250,100); SetColor(13); Circle(300,250,80); SetColor(10); Arc(300,250,135,45,60); {Рисуем дугу, X, Y, Ф1, Ф2, R} SetColor(12); Ellipse(300,250,0,360,95,40); {Рисуем эллипс, X, Y, Ф1, Ф2, R1, R2} PutPixel(300,250,15); {Рисуем точку, X, Y, C} SetColor(15); OutTextXY(25,30,'Графика в Turbo Pascal.'); {Вывод текста, X, Y, 'Текст'} SetColor(11); OutTextXY(160,450,'Для выхода из программы нажмите Esc.'); SetFillStyle(1,14); {Задаем вид закраски (0-11) и цвет закраски С} Bar(20,70,210,50); {Рисуем закрашенный прямоугольник, X1,Y1,X2,Y2} SetColor(11); Rectangle(25,100,100,200); {Рисуем прямоугольную рамку, X1,Y1,X2,Y2} SetColor(14); Line(25,100,100,200); {Рисуем прямую линию, X1,Y1,X2,Y2} Readkey; CloseGraph; end.   Здесь X, Y, X1, Y1, X2, Y2 - координаты основных точек на экране; Ф1, Ф2 - углы дуг, круговых и эллиптических секторов; R, R1, R2 - радиусы окружностей, эллипсов, дуг и секторов. С - цвет линий (0-15).   Пример 3. Флаг России.   program Flag_RUS; uses CRT,Graph,Graph0; begin Init('c:\tp7\'); SetFillStyle(1,15); Bar(0,0,320,50); SetFillStyle(1,1); Bar(0,51,320,101); SetFillStyle(1,4); Bar(0,102,320,152); ReadKey; CloseGraph; end.   Примеры программ построения графиков функций:   1. Построение графика параболы в декартовых координатах (путь S(t)=gt2/2 при свободном падении тела). Построение производится по точкам.   Program Put3; uses Crt,Graph,Graph0; var t1,S,H,n:integer;Y,g,dt,t:real; begin Init('c:\tp7\'); SetColor(14); OutTextXY(25,30,'Путь S(t)=gt2/2 при свободном падении.'); OutTextXY(25,50,'Выход - любая клавиша.'); SetColor(10); Line(0,470,550,470); Line(0,0,0,470); g:=9.81; t:=0; n:=100; repeat Y:=g*t*t/2; dt:=1/(n+1); t:=t+dt; t1:=round(6*t); S:=round(Y); H:=round(470-S/70); PutPixel(t1,H,11); until t>80; Readkey; CloseGraph; end.   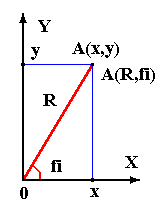2. Построение графика функции (улитки Паскаля) в полярных коорди- натах. Если в прямоугольных (декартовых) кординатах задают точку A на плоскости по её координатам x, y, то в полярных координатах точку задают по её радиус-вектору R и углу fi между вектором R и осью X (смотрите чертёж на рисунке). Функция в декартовых коорди- натах имеет вид y=f(x), в полярных координатах R=F(fi). Связь между декартовыми и полярными координатами: x=R*cos(fi), y=R*sin(fi), R=SQRT(x*x+y*y).   Program Ulitka; uses crt, graph, graph0; const xc=320; yc=175; k=0.775; var fi,dfi,R,a:real; x1,y1,x2,y2,n:integer; Function F(fi:real):real; begin F:=a/2+a*cos(fi); end; begin clrscr; writeln('Улитка Паскаля: R=1+a*cos(fi).'); write('Введите коэффициент a=0.5-2; a='); read(a); a:=100*a; write('Введите число точек n>=100; n='); read(n); init('C:\TP7\'); cleardevice; outtextxy(10,10,'Улитка Паскаля: R=1+a*cos(fi).'); setcolor(10); line(xc,0,xc,349); line(0,yc,639,yc); dfi:=2*pi/n; x1:=xc; y1:=yc; fi:=0; while fi<2*pi+dfi do begin R:=F(fi); x2:=xc+round(R*cos(fi)); y2:=yc+round(k*R*sin(fi)); setcolor(11); line(x1,y1,x2,y2); x1:=x2; y1:=y2; fi:=fi+dfi; end; outtextxy(10,30,'Выход - любая клавиша.'); readkey; closegraph; end.   Здесь построение графика функции производится с помощью отрезков прямых линий, которые при большом их числе превращаются в кривую линию. В программе для построения графика функции используется процедура Function, что позволяет строить графики других функций, не меняя программы (универсальный алгоритм), а заменив только вид самой функции R=F(fi). Например, если подставить R=a*(1-cos(fi)), то мы получим кардиоиду. Аналогично можно построить график спира- ли Архимеда R=a*fi и т.д.

Работа с файлами в Turbo Pascal При работе с файлами в TP используются следующие процедуры: assign(var F; name: string); - устанавливает соответствие между файлом и файловой переменной, окрывает все другие поцедуры работы с файлами. F -переменная любого файлового типа, name - полное имя файла. close(var F); - окончание процедур работы с файлами (закрытие файла). rewrite(var F: file); - создаёт и открывает новый файл. reset(var F: file); - открывает существующий файл. append(var F: text); - открывает существующий текстовый файл и позиционирует указатель обработки на конец файла. После этого можно дополнять текстовый файл информацией, начиная с конца стро- ки. erase(var F); - удаляет неоткрытый внешний файл любого типа, за- даваемый переменной F. rename(var F: newname: string); - переименовывает неоткрытый файл F любого типа. Новое имя задаётся строкой newname. Текстовый файл можно рассматривать как последовательность симво- лов, разбитую на строки длиной от 0 до 256 символов. Для описания используется стандартный тип text: var F: text; (F - файловая пе- ременная). Стандартные типы данных не требуют описания в разделе type в от- личие от типов, образованных пользователем. Формат раздела: type <имя типа> = <значение типа>; Имя и значение типа даёт пользователь. Пример: type fil=text;   Рассмотрим работу с файлами в TP на примерах.   Пример 1. Запись текстового файла на диск и ввод в него текста.   program wtf; type fil=text; var f1:fil; name:string[35]; txt:string; begin write('Введите имя файла для записи текста>'); readln(name); writeln; assign(f1,name); rewrite(f1); writeln('Введите текст для записи (для окончания-Enter):'); writeln; repeat write(':>'); readln(txt); writeln(f1,txt); until txt=''; close(f1); writeln; writeln('Ввод окончен, нажмите Enter.'); readln; end.   Пример 2. Запись результата вычисления в текстовый файл.   program wtf1; uses crt; type fil=text; var f1:fil; name:string[35]; txt:string; var i,n:real;s,q:real; begin clrscr; writeln('Для вычисления суммы ряда S=1+1/4+1/9+...+1/n2,'); write('введите n=1,2,3...: n='); read(n); i:=1; S:=1; while i<>n do begin i:=i+1; s:=s+1/(i*i); end; writeln('Сумма членов ряда равна S=',s); name:='rezult.txt'; txt:='Сумма ряда S=1+1/4+1/9+...+1/n2 равна: S='; writeln; assign(f1,name); rewrite(f1); writeln(f1,txt,s,' при n=',n:9:0); close(f1); writeln('Ваш результат будет записан в файл rezult.txt'); writeln('Для выхода из программы нажмите Enter.'); readkey; end.   Пример 3. Чтение последовательности длиной до 35 символов из текстового файла example.txt (его содержимое, например, "23456 Всем привет!"   Функция Eoln(var F: text) возвращает булевское значение True, если текущая файловая позиция находится на маркере конца строки или вызов Eof(F) возвратил значение True. Во всех других случаях значение функции будет False. Функция Eof(var F: text) возвращает булевское значение True, ес- ли указатель конца файла находится сразу за последним компонен- том. В противном случае - False.   program wtf2; var F: text; St: string[35]; begin assign(F, 'example.txt'); {Файл example.txt должен существовать!} reset(F); while not Eoln(F) do begin {Проверка конца строки} read(F,St); writeln('St = ',St); {Вывод на экран} end; readln(F); {Переход к следующей строке} close(F); writeln('Вывод символов из файла окончен. Для выхода - Enter.'); readln; end.

Численные методы и связанные с ними задачи. Рассмотрим некоторые характерные для численных методов задачи, для решения которых удобно использовать программирование на TP.   Пример 1. Вычислите приближенно определенный интеграл по формуле прямоугольников. Подынтегральная функция f(x)=sin(x). Пределы ин- тегрирования a=0; b=pi.   program INTEGRAL1; var i,n:integer; a,b,S,h,x,Y:real; begin writeln('Подынтегральная функция f(x)=sin(x). Пределы a=0; b=pi.'); write('Введите число членов ряда приближения: n='); read(n); a:=0; b:=pi; h:=(b-a)/n; S:=0; for i:=1 to n do begin x:=a+i*h-h/2; S:=S+h*sin(x) end; writeln('Приближенное значение интеграла равно: I=',S); writeln('Для выхода из программы введите число 1.'); readln(Y); end.   Пример 2. Вычислите выражение S=sqrt(1+sqrt(2+sqrt(3+sqrt(4+...))) с максимальной точностью.   program zp1; var j,n:integer;s0,s1:real; begin s0:=0; s1:=1; n:=1; while s0<>s1 do begin s0:=s1; n:=n+1; s1:=0; for j:=n downto 1 do s1:=sqrt(j+s1); end; writeln('Ответ: значение выражения S=',s1); writeln('Для выхода из программы - Enter.'); readln end.   Пример 3. Вычислите с точностью e (e<<1) сумму ряда S=sin(x)=x-x3/3!+x5/5!-x7/7!+...+(-1)(n-1)*x(2*n-1)/(2*n-1)! Это разложение функции S=sin(x) в ряд Тейлора.   program zp2; var i:integer;x,y,S,e,q:real; begin write('Введите x='); read(x); write('Введите величину точности e='); read(e); i:=1; S:=x; y:=x; while abs(y)>e do begin i:=i+1; y:=-y*x*x/((2*i-2)*(2*i-1)); S:=S+y; end; writeln('Ответ: Сумма ряда S=',S); writeln('Для сравнения и проверки S=sin(x)=',sin(x)); writeln('Для выхода из программы введите любое число.'); readln(q); end.   Пример 4. Решение уравнения F(x)=sin(x)-x+0.25=0 методом простых итерраций. Суть этого метода заключается в следующем. Пусть Xo - исходное приближённое значение корня уравнения F(x)=0, которое может быть переписано в виде x=f(x). Тогда в качестве следующего приближения примем x1=f(Xo). В качестве следующего приближения возьмём x2=f(x1). Продолжая процесс дальше, в качестве n-го приб- лижения необходимо положить Xn=f(X(n-1)). Итеррационный процесс будет сходиться и мы в итоге указанной процедуры найдем корень уравнения, если ABS(f'(x))<1. В противном случае процесс расхо- дится и мы не найдём решение этим методом. При нахождении исход- ного значения корня Xo следует учитывать, что в окрестности корня функция F(x) меняет знак. Данное уравнение можно решить только приближённо и лишь численны- ми методами. Заданная точность e=1e-9. Начальное значение корня x=1. Получаемый в процессе решения результат x=1.1712296519 прев- ращает уравнение в тождество с большой точностью.   program iterac; label m1; var i:integer; x,x1,e,q:real; begin e:=1e-9; x:=1; for i:=1 to 30 do begin x1:=sin(x)+0.25; if abs(x1-x)<=e then goto m1; x:=x1; end; m1: writeln('Ответ: x =',x1); writeln('Для выхода введите любое число.'); readln(q); end.   Пример 5. Решение уравнения F(x)=cos(x)-x=0 методом Ньютона. Согласно методу Ньютона, корень уравнения равен x1=x-F(x)/F'(x). Этот численный метод часто используется как основной, а также в тех случаях, когда уравнение не удаётся решить методом простых итерраций. Чтобы метод сходился и приводил к результату необходи- мо, чтобы начальное значение x было выбрано достаточно близко к корню и в окресности корня значение F'(x) не было слишком большим и F'(x) не было слишком близко к нулю. Последнее условие F'(x)<>0 означает, что никакие два корня не находятся слишком близко один к другому. В данном примере начальное значение корня x=0.7. Корень x=0.73908.   program Newton; uses crt; var x,x1,e:real; i:integer; begin clrscr; i:=1; e:=1E-3; x:=0.7; repeat i:=i+40; x:=x+i*e; x1:=x+(cos(x)-x)/(sin(x)+1); until abs(x-x1)>=e; writeln('Ответ: x=', x1); writeln('Проверка решения: F(x)=cos(x)-x =', cos(x1)-x1); writeln('Выход - любая клавиша.'); readkey; end.

Вопросы 1. Что такое данные логического типа и как они используются? 2. Какие существуют операции отношений над переменными в Turbo Pascal? 3. Какие существуют операции над данными логического типа? 4. Что такое данные символьного типа? 5. Что такое данные строкового типа? 6. Что такое библиотека CRT в Turbo Pascal и как она используется? 7. Какие директивы модуля CRT вы знаете? 8. Как очищается экран и задается цвет текста и цвет фона? 9. Как устанавливается и отключается звуковой сигнал? 10. Что такое модуль Graph и какие директивы модуля Graph Вы знаете?   Задания 1. Воспроизведите самостоятельно и проанализируйте приведенную выше программу исследования треугольника. 2. Составьте программу, определяющую наибольшее из трёх чисел. 3. Составьте программу, определяющую наименьшее из трёх чисел. 4. Введите в приведенные выше программы модуль CRT и задайте цвет текста и цвет фона, а затем поменяйте их. Примените команду очистки экрана. 5. Введите в приведенные выше программы модуль CRT и задайте включение звука, измените частоту и длительность его звучания. Попытайтесь исполнить простейшую мелодию, а затем отключите звук. 6. Создайте простейшие изображения (окружность, линия, прямоу- гольник, эллипс) при помощи модуля Graph Turbo Pascal. 7. Нарисуйте треугольник с вписанной и описанной окружностями. 8. Нарисуйте квадрат с диагоналями и с вписанной в него окруж- ностью. 9. Нарисуйте Солнце. 10. Нарисуйте пятиконечную звезду, вписанную в окружность. 11. Нарисуйте график функции (параболы, гиперболы и т.д.). 12. Решите уравнение методом простых итерраций: exp(x)+x=0 (Ответ: x=-0.567) 13. Решите следующие уравнения методом Ньютона: 2*x3-5*x2+5*x-3=0 (Ответ: x=1.5); x3-x2-x-2=0 (Ответ: x=2); exp(x)+x-3=0 (Ответ: x=0.792) 14. Вычислите простейшие определённые интегралы методом прямоугольников от следующих функций: cos(x) от 0 до pi/2 (Ответ: S=1) 1/x от 1 до e (Ответ: S=1) 4/(1+x2) от 0 до 1 (Ответ: S=pi) exp(x) от 0 до 1 (Ответ: S=e-1).

Хостинг от uCoz